Im Folgenden wird die Theorie für die Implementierung der Matrix-Produkt-Zustände (MPS) und der Matrix-Produkt-Operatoren (MPO) beschrieben. Hierbei wird sich stark an den Artikel “The density-matrix renormalization group in the age of matrix product states” von Ulrich Schollwöck¹⁾ gehalten.

Betrachtet man eine 1-dimensionale Spin-\(\frac{1}{2}\)-Quantenkette mit \(L\) Plätzen und offenen Rändern, die an jedem Platz \(i\) den Zustand \(\sigma_i=\{\uparrow, \downarrow\}\) annehmen kann, so kann man den Quantenzustand auf dieser Kette als Summe über die Basiszustände darstellen:

\begin{align} \lvert\psi\rangle = \sum_{\sigma_1, \ldots, \sigma_L} c_{\sigma_1\ldots\sigma_L} \lvert {\sigma_1, \ldots, \sigma_L} \rangle \end{align} Hierbei sind die Koeffizienten \(c_{\sigma_1\ldots\sigma_L} \in \mathbb{C}\). Die Anzahl der Koeffizienten $c_{\sigma_1\ldots\sigma_L}$ steigt exponentiell (\(2^L\)) mit der Länge der Kette an. MPS stellen jeden dieser Koeffizienten als Matrix-Produkt dar, die Matrizen sind hierbei nur lokal für jeweils einen Platz definiert. 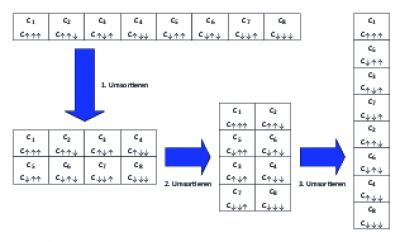Um einen MPS aus einem bekannten Quantenzustand mit Koeffizienten \(c_{\sigma_1\ldots\sigma_L} \in \mathbb{C}\) zu erzeugen, müssen im ersten Schritt die \(2^L\) Koeffizienten in eine Matrix \(c^\prime\) der Dimension \(2 \times 2^{L-1}\) umsortiert werden: \begin{align} c_{\sigma_1\ldots\sigma_L}^{\phantom\prime} = c_{\sigma_1, (\sigma_2\ldots\sigma_L)}^\prime \end{align} Auf die Matrix \(c^\prime\) wird dann eine Single-Value-Decomposition (SVD)²⁾ angewandt: \begin{align} c_{\sigma_1, (\sigma_2\ldots\sigma_L)}^\prime = \sum_{a_1}^{r_1} U_{\sigma_1, a_1}^{\phantom\prime} S_{a_1, a_1}^{\phantom\prime} (V^{\phantom\prime\dagger})_{a_1, (\sigma_2\ldots\sigma_L)} \end{align} Aus \(S\) und \(V^\dagger\) wird ein neues \(\tilde c_{a_1\sigma_2\ldots\sigma_L}^\prime\) erzeugt, welches dann wiederum in eine Matrix \(c_{(a_1\sigma_2),(\sigma_3\ldots\sigma_L)}^{\prime\prime}\) umsortiert wird. Darüber hinaus wird die Matrix \(U\), für die \(U^\dagger U = \mathbb{1}\) gilt, in zwei \(A^{\sigma_1}\)-Matrizen umsortiert. Die Einträge der \(A\)-Matrix ergeben sich zu \(A^{\sigma_1}_{1,a_1}=U_{\sigma_1,a_1}\).
Man erhält: \begin{align} c_{\sigma_1,\ldots\, \sigma_L}=\sum_{a_1}A_{1,a_1}^{\sigma_1}c_{(a_1\sigma_2),(\sigma_3\ldots\sigma_L)}^{\prime\prime} \end{align} Nun wird auf \(c_{(a_1\sigma_2),(\sigma_3\ldots\sigma_L)}^{\prime\prime}\) wiederum eine SVD angewandt. Das \(S\) und \(V^\dagger\) werden wieder zu einer Matrix zusammengefasst und das entstehende \(U\) wieder in zwei \(A\)-Matrizen umsortiert. Die Einträge ergeben sich jetzt zu \(A^{\sigma_2}_{a_1,a_2} = U_{(a_1\sigma_2), a_2}\).
Dies wird solange wiederholt, bis der Platz \(L-1\) erreicht ist. An dieser Stelle hat man dann: \begin{align*} c_{\sigma_1,\ldots\, \sigma_L} &=\sum_{a_1}\cdots\sum_{a_{l-1}}A_{1,a_1}^{\sigma_1}\cdots A_{a_{l-2},a_{l-1}}^{\sigma_{l-1}}\underbrace{c_{(a_{l-1}\sigma_{l}), (\sigma_{l+1}\ldots\sigma_L)}^{\prime\cdots\prime}}_{M_{a_{L-1},a_L}^{\sigma_L}}\newline &=A^{\sigma_1}\cdots A^{\sigma_{L-1}}M^{\sigma_L} \end{align*} Hierbei erfüllen alle \(A\)-Matrizen die Bedingung für links-Normierung \(\sum_{\sigma_l}A^{\sigma_l\dagger}A^{\sigma_l}= \mathbb{1}\). Analog dazu kann man einen rechts-normierten MPS erzeugen, indem man \(V^\dagger\) in \(B\)-Matrizen umformt und \(U\) und \(S\) jeweils weiterverwendet. Alle \(B\)-Matrizen erfüllen dann die Bedingung für rechts-Normierung \(\sum_{\sigma_l}B^{\sigma_l}B^{\sigma_l\dagger}= \mathbb{1}\). Einen gemischt-normierten Zustand erhält man, wenn man von beiden Seiten beginnt und am Platz \(l\) das \(U\) und das \(S\) bzw. das \(S\) und das \(V^\dagger\) zu einer Matrix \(M\) umformt. Die Matrix \(M^{\sigma_l}\) erfüllt keine Normierungsbedingung.
Ein so entwickelter MPS ist eine exakte Darstellung des Zustandes. Ein entscheidender Vorzug der MPS besteht aber darin, dass man die maximale Dimension \(d_{\text{max}}\) der Matrizen begrenzen kann und trotzdem eine sehr gute Näherung an den exakten Zustand erhält.

Das Skalarprodukt stellt sich in MPS-Schreibweise folgendermaßen dar: \begin{equation*} \langle \phi \lvert \psi \rangle = \sum_{\boldsymbol{\sigma\sigma^\prime}}\langle \boldsymbol{\sigma^\prime} \lvert \tilde{M}^{\sigma_1^\prime *}\cdots\tilde{M}^{\sigma_L^\prime *}M^{\sigma_1^{\phantom\prime}}\cdots M^{\sigma_L^{\phantom\prime}}\lvert \boldsymbol{\sigma} \rangle \end{equation*} Dies lässt sich, da die \(\sigma_i^{\phantom\prime}\) orthogonale Basisvektoren sind, zusammenfassen zu \begin{equation*} \langle \phi \lvert \psi \rangle = \sum_{\boldsymbol{\sigma}}\tilde{M}^{\sigma_1*}\cdots\tilde{M}^{\sigma_L *}M^{\sigma_1}\cdots M^{\sigma_L} \end{equation*} Um diesen Ausdruck zu berechnen, müsste man \(2^L\) Matrixprodukte summieren, die jeweils aus \(2L-1\) Matrixmultiplikationen bestehen. Das bedeutet, dass der Aufwand exponential mit der Länge der Kette steigt. Wenn man den Ausdruck allerdings umschreibt, reduziert sich der Aufwand auf \(2L\) Additionen und \(4L-2\) Matrixmultiplikationen, was einem polynomial zur Kettenlänge steigenden Aufwand entspricht: \begin{equation*} \langle \phi \lvert \psi \rangle = \sum_{\sigma_L}\tilde{M}^{\sigma_1\dagger}\left(\cdots\left(\sum_{\sigma_2}\tilde{M}^{\sigma_2\dagger}\left(\sum_{\sigma_1}\tilde{M}^{\sigma_1\dagger}M^{\sigma_1}\right)M^{\sigma_2}\right)\cdots\right) M^{\sigma_L} \end{equation*}

Jeder Operator kann als Matrix-Produkt-Operator geschrieben werden: \begin{eqnarray*} \hat O & = & \sum_{\boldsymbol{\sigma}, \boldsymbol{\sigma^{\prime}}} c_{(\sigma_1^{\phantom\prime}\ldots\sigma_L^{\phantom\prime})(\sigma_1^{\prime}\ldots\sigma_L^{\prime})} \lvert {\boldsymbol{\sigma}} \rangle \langle {\boldsymbol{\sigma'}} \lvert \newline & = & \sum_{\boldsymbol{\sigma}, \boldsymbol{\sigma^{\prime}}} c_{(\sigma_1^{\phantom\prime}\sigma_1^{\prime})\ldots(\sigma_L^{\phantom\prime}\sigma_L^{\prime})} \lvert {\boldsymbol{\sigma}} \rangle \langle {\boldsymbol{\sigma^{\prime}}} \lvert \newline & = & \sum_{\boldsymbol{\sigma}, \boldsymbol{\sigma^{\prime}}} W^{\sigma_1^{\phantom\prime}\sigma_1^{\prime}}\ldots W^{\sigma_L^{\phantom\prime}\sigma_L^{\prime}} \lvert {\boldsymbol{\sigma}} \rangle \langle {\boldsymbol{\sigma^{\prime}}} \lvert \newline \end{eqnarray*} Hierbei nehmen die \(W\)-Matrizen die Rolle der \(M\)-Matrizen eines MPS ein. Der Unterschied besteht darin, dass sie einen weiteren Index und somit eine weitere Dimension besitzen.

Beim Anwenden eines MPO auf einen MPS kann der Ausdruck wieder stark zusammengefasst werden: \begin{eqnarray*} \hat O \lvert \psi \rangle & = & \sum_{\boldsymbol{\sigma}, \boldsymbol{\sigma^{\prime}}, \boldsymbol{\sigma^{\prime\prime}}} (W^{\sigma_1^{\phantom\prime}\sigma_1^{\prime}}\ldots W^{\sigma_L^{\phantom\prime}\sigma_L^{\prime}})(M^{\sigma_1^{\prime\prime}}\cdots M^{\sigma_L^{\prime\prime}})\lvert {\boldsymbol{\sigma}} \rangle \underbrace{\langle {\boldsymbol{\sigma^\prime}} \lvert {\boldsymbol{\sigma^{\prime\prime}}} \rangle}_{\delta_{\sigma^{\prime}\sigma^{\prime\prime}}} \newline & = & \sum_{\boldsymbol{\sigma}, \boldsymbol{\sigma^{\prime}}} (W^{\sigma_1^{\phantom\prime}\sigma_1^{\prime}}\ldots W^{\sigma_L^{\phantom\prime}\sigma_L^{\prime}})(M^{\sigma_1^{\prime\prime}}\cdots M^{\sigma_L^{\prime\prime}})\lvert {\boldsymbol{\sigma}} \rangle \newline & = & \sum_{\boldsymbol{\sigma}} \tilde{M}^{\sigma_1^{\phantom\prime}}\cdots \tilde{M}^{\sigma_L^{\phantom\prime}} \lvert\boldsymbol{\sigma}\rangle = \lvert \tilde\psi\rangle \end{eqnarray*} Die Einträge der \(\tilde{M}\)-Matrix sind gegeben durch: \begin{equation*} \tilde{M}^{\sigma_i^{\phantom\prime}} = \sum_{\sigma_i^{\prime}}W^{\sigma_i^{\phantom\prime}\sigma_i^{\prime}}_{b_{i-1},b_i}M^{\sigma_i^{\prime}}_{a_{i-1}, a_i} \end{equation*} \(\lvert \tilde\psi\rangle\) stellt somit wiederum einen MPS dar. Allerdings ist die Dimension der \(\tilde{M}\)-Matrizen das Produkt der Dimensionen der MPS-Matrizen und der MPO-Matrizen.
Auf diesem Weg lässt sich der Erwartungswert eines Operators bestimmen: \begin{equation*} \langle \psi \lvert \hat O \lvert \psi \rangle = \langle \psi \lvert \tilde \psi \rangle \end{equation*} Wiederholtes Anwenden eines MPO auf einen MPS führt dazu, dass die Dimension des entstehenden MPS immer weiter ansteigt.

Da sich jeder Operator als MPO darstellen lässt, muss dies auch für einen Hamilton-Operator \begin{equation*} \hat H = J\sum_{i=1}^{L-1}\frac{1}{2}\hat S_i^+\hat S_{i+1}^- + \frac{1}{2}\hat S_i^-\hat S_{i+1}^+ + J^z\hat S_i^z\hat S_{i+1}^z-h_z\sum_i^L \hat S_i^z-h_x\sum_i^L \hat S_i^x \end{equation*} gelten. Hierbei stehen \(J\) und \(J^z\) für die Kopplungskonstanten der Spins und \(h^z\) und \(h^x\) für Stärke der Magnetfelder in der entspechenden Richtung. Dass sich dieser MPO allerdings explizit, mit einer geringen Dimension, konstruieren lässt, ist der Tensor-Produkt-Struktur des Hamilton-Operators zu verdanken: \begin{equation*} \hat H = J^z\hat S_1^z\otimes\hat S_2^z\otimes\hat I_3\otimes\hat I_4\ldots + \hat I_1\otimes J^z\hat S_2^z\otimes\hat S_3^z\otimes\hat I_4\ldots+\ldots \end{equation*} Um den Hamilton-Operator als MPO konstruieren zu können, muss dieser zunächst in Operatoren, die jeweils auf einen Platz wirken, zerlegt werden. Hierzu werden die Operatoren \begin{equation*} \hat W^{\left[i\right]}=\sum_{\sigma^{\phantom\prime}_i, \sigma^\prime_i}W^{\sigma_i^{\phantom\prime}\sigma_i^\prime}\lvert\sigma_i^{\phantom\prime}\rangle\langle\sigma_i^{\prime}\lvert \end{equation*} eingeführt. Diese haben, für den oben beschriebenen Hamiltonian, folgende Form: \begin{equation*} \hat W^{\left[i\right]} = \begin{bmatrix} \hat I & 0 & 0 & 0 & 0\newline \hat S^+ & 0 & 0 & 0 & 0\newline \hat S^- & 0 & 0 & 0 & 0\newline \hat S^z & 0 & 0 & 0 & 0\newline -h_z\hat S^z-h_x\hat S^x & (J/2)\hat S^- & (J/2)\hat S^+ & J^z\hat S^z & \hat I \end{bmatrix} \end{equation*} Zwei Ausnahmen bilden die Operatoren für den ersten und den letzten Platz: \begin{equation*} \hat W^{\left[1\right]} = \begin{bmatrix} -h_z\hat S^z-h_x\hat S^x & (J/2)\hat S^- & (J/2)\hat S^+ & J^z\hat S^z & \hat I \end{bmatrix} \quad \hat W^{\left[L\right]} = \begin{bmatrix} \hat I \newline \hat S^+ \newline \hat S^- \newline \hat S^z \newline -h_z\hat S^z-h_x\hat S^x \end{bmatrix} \end{equation*} Entsprechend der Konstruktion der \(\hat W^{\left[i\right]}\) können die \(W^{\sigma_i^{\phantom\prime},\sigma_i^\prime}\) bestimmt werden: \begin{equation*} \hat W^{\sigma_i^{\phantom\prime}\sigma_i^{\prime}}_{j, k} = \langle\sigma_i\lvert \hat W^{\left[i\right]}_{j, k} \lvert \sigma_i'\rangle \end{equation*}

©: This site was created by Thomas Köhler