Im Folgenden werden die Ergebnisse des Applets für verschiedener Modelle mit z.T. bekannten analytischen Lösungen verglichen. Um die Werte reproduzieren zu können, wird das Applet mit einem Link jeweils mit den nötigen Daten aufgerufen.

Das Ising-Modell ist ein nach Ernst Ising benanntes Modell zur Beschreibung von Ferro- und Antiferromagnetismus in Festkörpern. Es beschreibt die Wechselwirkung benachbarter Spins. Diese Spins stellen die Ursache für den Anti- bzw. Ferromagnetismus dar. Es wird ausgenutzt, dass für die magnetischen Momente keine Raumrichtung ausgezeichnet ist und daher eine beliebige Richtung gewählt werden kann ¹⁾. Üblicherweise wird die z-Achse ausgewählt ²⁾. Im isotropen, d. h. magnetfeldfreien, ein-dimensionalen Fall existiert kein Phasenübergang, wie die exakte Lösung zeigt³⁾. Im zweidimensionalen Fall existieren dahingegen Phasenübergänge ^{4) 5)}. Für höhere Dimensionen gibt es bisher keine exakten Lösungen, allerdings existiert ein Beweis für die Existenz von Phasenübergängen ⁶⁾.

Der Hamilton-Operator \(\hat H\) für das Ising-Modell ohne Magnetfeld mit konstanter Nächster-Nachbar-Wechselwirkung und offenen Randbedingungen lautet: \begin{equation*} \hat H= J^z\sum_{i=1}^{N-1}\hat S_i^z \hat S_{i+1}^z \end{equation*} Die Grundzustandsenergie beträgt für eine Kette mit N Plätzen: \begin{equation*} E_0 = -\frac{(N-1)\cdot \lvert J^z\lvert}{4} \end{equation*} Dies kann, beispielhaft für eine Kette mit 8 Plätzen betrachtet werden. Hier ausprobieren

Ist \(J>0\) so beschreibt der Hamilton-Operator einen Antiferromagneten. Das bedeutet, dass sich alle Spins im Grundzustand entgegengesetzt zueinander ausrichten. \begin{equation*} \lvert\psi\rangle = \lvert\uparrow\downarrow\uparrow\ldots\rangle \quad \text{oder} \quad \lvert\psi\rangle = \lvert\downarrow\uparrow\downarrow\ldots\rangle \end{equation*} Dies wird als Néelzustand bezeichnet. Der Grundzustand kann eine beliebige Linearkombination dieser beiden Zustände sein, in der DMRG wird allerdings immer einer dieser beiden ausgewählt. Die Auswahl einer der beiden Möglichkeiten erfolgt in der DMRG nicht vorhersehbar. Es kann auch sprunghaft zwischen beiden gewechselt werden. Der Erwartungswert von \(\hat S_i^z\) am Platz \(i\) lautet: \begin{equation*} \langle\hat S_i^z\rangle=\pm \frac{1}{2} \end{equation*} Da beide Erwartungswerte abwechselnd auftreten, lautet der Erwartungswert für \(\hat S^z\): \begin{equation*} \langle\hat S^z\rangle=\left\{\begin{array}{cl} 0, & \text{falls }N \text{ gerade}\newline \pm \frac{1}{2}, & \text{falls }N \text{ ungerade} \end{array}\right. \end{equation*} Ein Beispiel hierfür kann hier und hier ausprobiert werden.

Ist \(J<0\) handelt es sich um einen Ferromagneten. Bei diesem sind die Spins im Grundzustand parallel zueinander ausgerichtet: \begin{equation*} \lvert\psi\rangle = \lvert\uparrow\uparrow\uparrow\ldots\rangle \quad \text{oder} \quad \lvert\psi\rangle = \lvert\downarrow\downarrow\downarrow\ldots\rangle \end{equation*} Auch hier ist der Grundzustand eine Linearkombination der beiden Zustände, wobei die DMRG wiederum unvorhersehbar einen auswählt. Der Erwartungswert von \(\hat S_i^z\) entspricht dem im antiferromagnetischen Fall. Der Erwartungswert von \(\hat S^z\) lautet: \begin{equation*} \langle\hat S^z\rangle=\pm \frac{N}{2} \end{equation*} Ein Beispiel für den hierfür kann hier ausprobiert werden.

Um den Hamilton-Operator \(\hat H\) des Ising-Modells um ein longitudinales Magnetfeld zu erweitern, wird ein zusätzlicher Term in z-Richtung hinzugefügt: \begin{equation*} \hat H= J^z\sum_{i}\hat S_i^z \hat S_{i+1}^z + h^z\hat S_i^z \end{equation*} Hierbei gibt \(h^z\) die Stärke des Magnetfeldes an. %Im Folgenden wird zunächst angenommen, dass \(h^z\ll J^z\) gilt. Der Antiferromagnet zeigt einen Phasenübergang zum Ferromagneten bei \(h^z_c = J^z\). Der Ferromagnet dahingegen weisst keinen Phasenübergang auf.

Gilt \(h^z\ll J^z\), so gibt das Vorzeichen des Magnetfelds \(h^z\) im antiferromagnetischen Fall für eine Kette mit einer ungeraden Anzahl an Plätzen die Ausrichtung der äußeren beiden Spins vor. \begin{equation*} \lvert\psi\rangle=\left\{\begin{array}{cl} \lvert\uparrow\downarrow\uparrow\cdots\downarrow\uparrow\rangle, & \text{falls }h^z < 0\newline \lvert\downarrow\uparrow\downarrow\cdots\uparrow\downarrow\rangle, & \text{falls }h^z>0 \end{array}\right. \end{equation*} Um diesen Fall zu untersuchen bitte hier und/oder hier klicken.

Für Ketten mit gerader Anzahl an Plätzen beträgt die Grundzustandsenergie: \begin{equation*} E_0=\left\{\begin{array}{cl} -\frac{N-1}{4}\lvert J^z\lvert, & \text{falls }h^z \leq \frac{J^z}{2} \text{, Antiferromagnet: }\lvert\uparrow\downarrow\uparrow\cdots\uparrow\downarrow\rangle \newline -\frac{N-3}{4}\lvert J^z\lvert - \lvert h^z\lvert, & \text{falls }\frac{J^z}{2}< h^z\leq J^z \text{, defekter Antiferromagnet: }\lvert\uparrow\downarrow\uparrow\cdots\uparrow\uparrow\rangle\newline \frac{N-1}{4}\lvert J^z\lvert - \frac{N}{2}\lvert h^z\lvert, & \text{falls }J^z< h^z \text{, Ferromagnet: }\lvert\uparrow\uparrow\uparrow\cdots\uparrow\uparrow\rangle\end{array}\right. \end{equation*} Im Fall einer ungeraden Anzahl an Kettenplätzen beträgt die Grundzustandsenergie: \begin{equation*} E_0=\left\{\begin{array}{cl} -\frac{N-1}{4}\lvert J^z\lvert - \frac{\lvert h^z\lvert}{2}, & \text{falls } h^z\leq J^z \text{, Antiferromagnet: }\lvert\uparrow\downarrow\uparrow\cdots\uparrow\rangle\newline \frac{N-1}{4}\lvert J^z\lvert - \frac{N}{2}\lvert h^z\lvert, & \text{falls }J^z< h^z \text{, Ferromagnet: }\lvert\uparrow\uparrow\uparrow\cdots\uparrow\uparrow\rangle\end{array}\right. 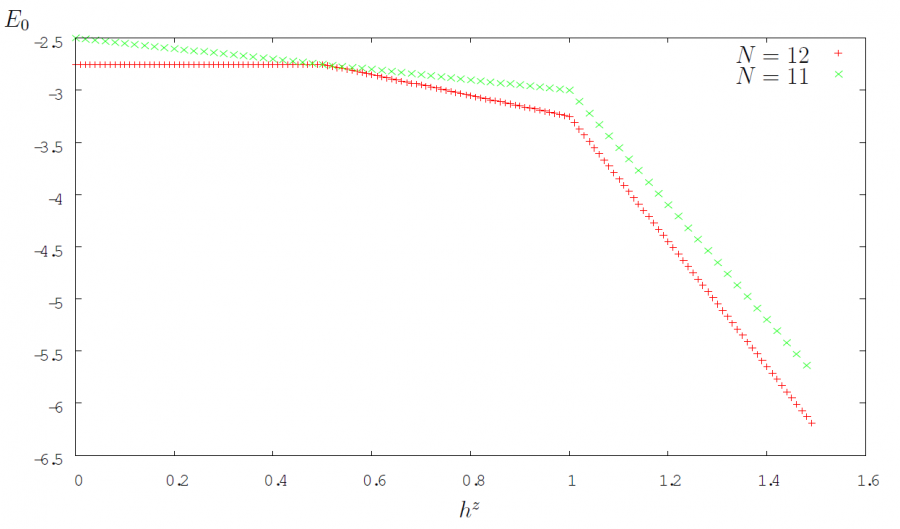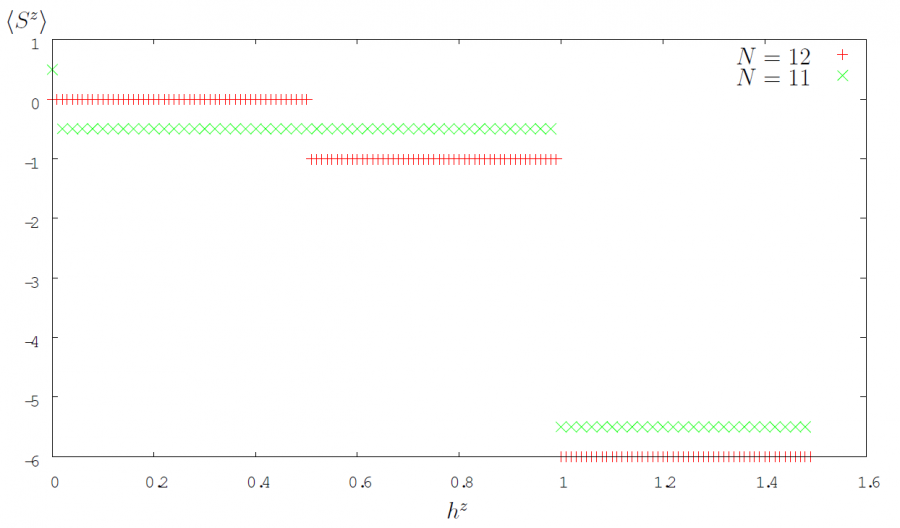\end{equation*} Diese Fallunterscheidungen, sind damit zu erklären, dass ab einer Feldstärke \(h^z \leq h^z_c\) das externe Magnetfeld stärker als die inneren Wechselwirkungen ist und es somit energetisch günstiger ist, dem Magnetfeld zu folgen. Der mittlere Fall für Ketten mit gerader Anzahl an Plätzen ist den offenen Randbedingungen geschuldet, da hierdurch zunächst nur der Rand-Spin am Magnetfeld ausgerichtet wird. Dies ist daran zu erkennen, dass es sich nur um eine kleine Veränderung handelt. In den folgenden beiden Abbildungen sind diese zwei bzw. drei Bereiche gut zu erkennen. [] []

In diesem Fall gibt das Vorzeichen von \(h^z\) immer die Ausrichtung der Spins an. \begin{equation*} \lvert\psi\rangle=\left\{\begin{array}{cl} \lvert\uparrow\uparrow\uparrow\rangle, & \text{falls }h^z < 0\newline \lvert\downarrow\downarrow\downarrow\rangle, & \text{falls }h^z>0 \end{array}\right. \end{equation*} Der Erwartungswert von \(S^z\) wird ebenfalls durch \(h^z\) festgelegt. \begin{equation*} \langle\psi\lvert\hat S^z\lvert\psi\rangle=\left\{\begin{array}{cl} \frac{N}{2}, & \text{falls }h^z < 0\newline -\frac{N}{2}, & \text{falls }h^z>0 \end{array}\right . \end{equation*} Die Grundzustandsenergie beträgt: \begin{equation*} E_0 = -\frac{(N-1)\cdot \lvert J\lvert}{4} - \lvert h^z \lvert\frac{N}{2} \end{equation*} Da sich die Abbildungen nur minimal von denen im ferromagnetischen Fall ohne Magnetfeld unterscheiden würden, wird an dieser Stelle auf weitere Abbildungen verzichtet.

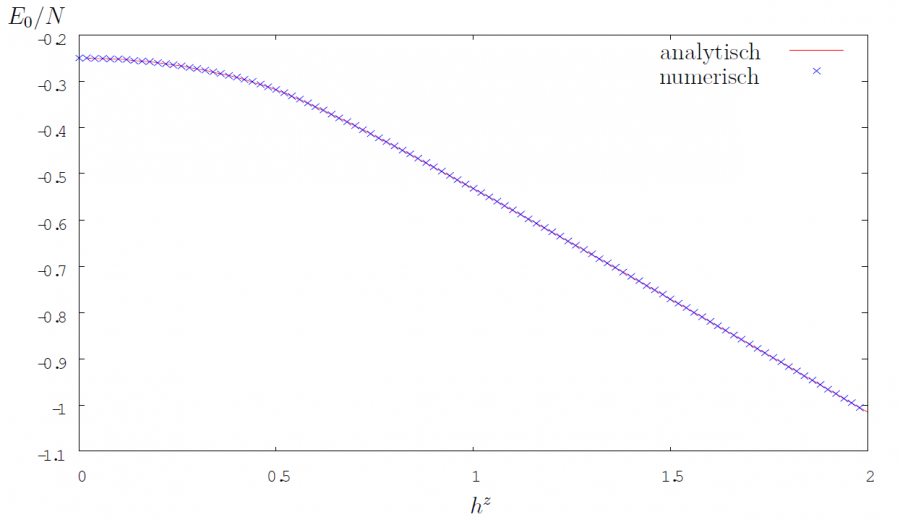
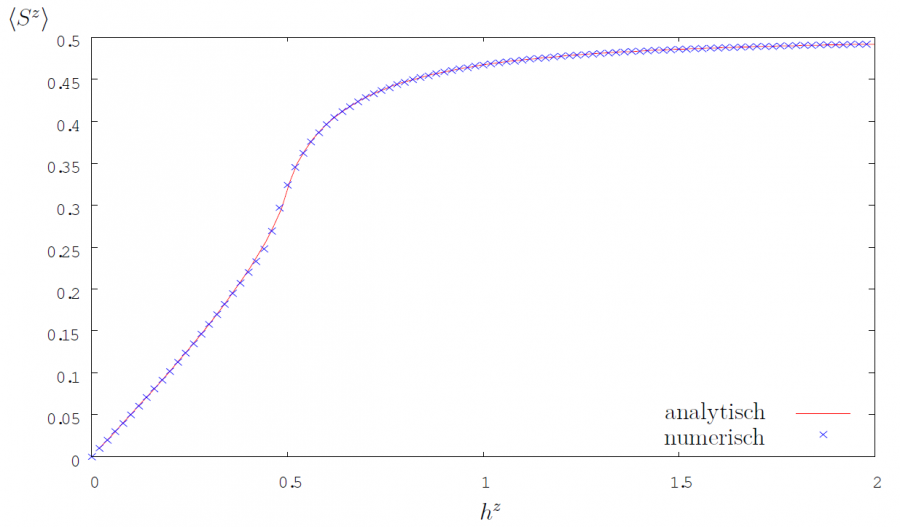
Der Hamilton-Operator für das Ising-Modell mit transversalem Magnetfeld lautet: \begin{equation*} \hat H= J^x\sum_{i}\hat S_i^x \hat S_{i+1}^x + h^z\hat S_i^z \end{equation*} Dieses System wurde exakt gelöst⁷⁾ und hat einen Phasenübergang bei \(h^z = J^x/2\). Um diesen Phasenübergang veranschaulichen zu können, werden systemgrößenbereinigte Werte für die Grundzustandsenergie und die Erwartungswerte verwendet (finite-size-scaling). Um diese zu bestimmen, werden zunächst \(E_0/N\), \(\langle S^x\rangle/N\) und \(\langle S^z\rangle/N\) gegen \(1/N\) für verschiedene \(h^z\) aufgetragen. Hieraus kann dann, mittels linearer Regression, ein größenbereinigtes \(E_0(h^z)\), \(\langle S^x\rangle (h^z)\) und \(\langle S^x\rangle (h^z)\) bestimmt werden. Diese größenbereinigten Werte werden in den folgenden Abbildungen gegen \(h^z\) aufgetragen. Hierbei liefert ⁸⁾ analytische Lösungen für die Grundzustandsenergie und den Erwartungswert von \(S^z\) in Abhängigkeit von \(\lambda=J/2h^z\): \begin{equation*} \frac{E_0}{J^xN}(\lambda)=\frac{2}{\pi}(1+\lambda)E\left(\frac{\pi}{2}, \Theta\right) \end{equation*} Hierbei ist \(\Theta^2=\frac{4\lambda}{(1+\lambda)^2}\) und \(E\left(\frac{\pi}{2}, \Theta\right)\) ein elliptisches Integral zweiter Art. \begin{equation*} \langle \hat S^z \rangle (\lambda) = \frac{1}{2}G(0, \lambda)\quad\text{mit }G(n,\lambda )=L(n,\lambda )+\lambda L(n+1,\lambda ) \end{equation*} Hier ist \(G(n,\lambda )=L(n,\lambda )+\lambda L(n+1,\lambda )\) wobei \begin{equation*} L(n,\lambda )=1/\pi \int_0^\pi dk \Lambda_k^{-1}cos(k n) \end{equation*} mit \(\Lambda_k^2=1+\lambda^2+ \lambda \cos(k)\) proportional zu einem elliptischen Integral erster Art ist. In den Abbildungen ist zu erkennen, dass die numerischen Ergebnisse den analytischen entsprechen.

[] []

Das Heisenberg-Modell verallgemeinert die im Ising-Modell auf eine Raumrichtung festgelegten Spins in alle Raumrichtungen. Da die Anzahl der Freiheitsgrade hierdurch ansteigt, ist die Berechnung deutlich aufwendiger. Daher wird in den meisten Fälle hiermit die exakte Lösbarkeit geopfert. Mit dem Bethe-Ansatz⁹⁾ kann das ein-dimensionale Heisenberg-Modell allerdings gelöst werden. Der Hamilton-Operator einer Kette im Heisenberg-Modell lautet: \begin{equation*} \hat H = J\sum_i \left(\hat S^x_i \hat S^x_{i+1} + \hat S^y_i \hat S^y_{i+1} + \hat S^z_i\hat S^z_{i+1}\right) \end{equation*} Für den ferromagnetischen Fall ist die Grundzustandsenergie identisch zum Ising-Modell (ohne Magnetfeld). Der Erwartungswert von \(S^z_i\) befindet sich im Intervall \([-0.5, 0.5]\). Die Grundzustandsenergie pro Platz bzw. pro Bindung ist für den antiferromagnetische Fall im folgenden Plot abgebilde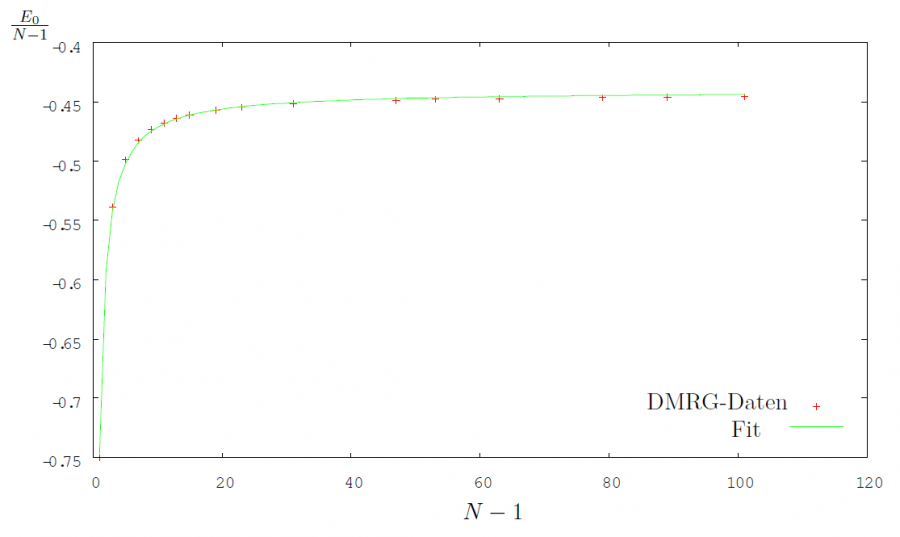t: [] Der Fit liefert eine Grundzustandenergie von \(-0.4407\pm0.00057\) pro Bindung für eine unendlich lange Kette. Mit dem Bethe-Ansatz erhält man \(\frac{1}{4}-ln(2)=-0.443147\). Der berechnete Wert liegt somit relativ nah am analytischen Wert.

©: This site was created by Thomas Köhler